1. Simple Empirical Density Functions
  2. Joint Distributions
  3. Tables
  4. Glyph Size

Lab 2 — Site Variables

Last lab we focused on obtaining and performing basic summary analyses of the vegetation data for Bryce Canyon National Park. In this lab we want to perform the complement, to import and analyze the environmental or site data for the same plots. First, the data are available at:

brycesite.R

To get the data into R as a data frame, click on the file name above to load a local copy, and then do the following:

site = read.table('brycesit.R',header=TRUE)
to get the site data into a data frame, and then
summary(site)
to familiarize yourself with the site variables

To look at these data, it is easier to attach the data frame. As you will recall from R for Ecologists, attaching a dataframe allows us to eliminate the dataframe name and field specifier "$" when using a specific field in the data frame.

attach(site)

Note from Jim: you'll need to delete some of the rows that contain spurious characters. You can do this by finding the row and then using: site=site[-14,] where 14 is the row to be deleted.

Simple Empirical Cumulative Density Function (ECDF) Plots of Site Variables

Let's look at the ECDF distributions of the continuous site variables first.

The "plot()" command below needs a second parameter for the values in the other axis of the scatter plot. A sequence with the same number of rows works (i.e. 1:156]). You can get the length of the "elev" row with "length()".

Also, the "lines()" function does not appear to draw but "segments(min(elev),1,max(elev),156)" will work where 156 is the number of rows in elev.


plot(sort(elev))                     # to see elevation distribution

lines(c(1,160),range(elev),col=2)    # to overlay a straight line of perfect 

                                     # distribution

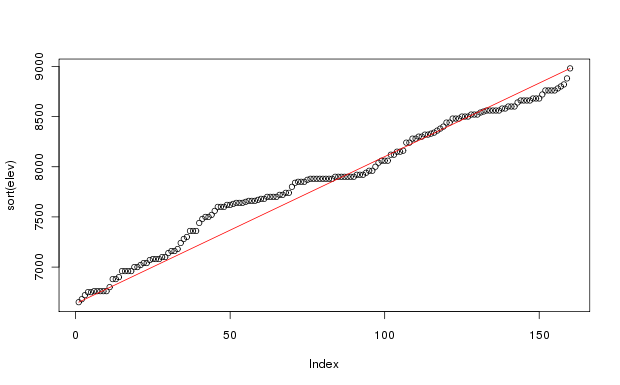
As you can see, the elevations of the sample plots are fairly uniformly spread from 6650 feet to 8980 feet (2027 to 2737 m). (Calculate elevm <- elev * 0.3048 to convert feet to meters). There are a few too few sample plots below 8000 feet, but the sample stratification took into account the variability of the vegetation by elevation, and lower elevations required fewer plots to represent them sufficiently. The

lines(c(1,160),range(elev),col=2)
command is an example of adding points or lines to an existing plot. Had I used plot() rather then lines() then R would have erased the plot I was adding to. The lines() command has two (or optionally more) arguments: (1) the X coefficients, and (2) the Y coefficients. The c(1,160) serves as the X axis coordinates (1 and 160) (remember, the c function stands for "combine", and makes a vector out of its arguments, and the range(elev) argument returns two values, the min and max of the specified vector. The length of the X and Y arguments must match exactly. The col=2 argument specifies that R should draw the line in whatever color is currently assigned to position 2 in the color vector.
plot(sort(av)) # to see aspect value = (cos((asp-30)/180*pi)+1)/2

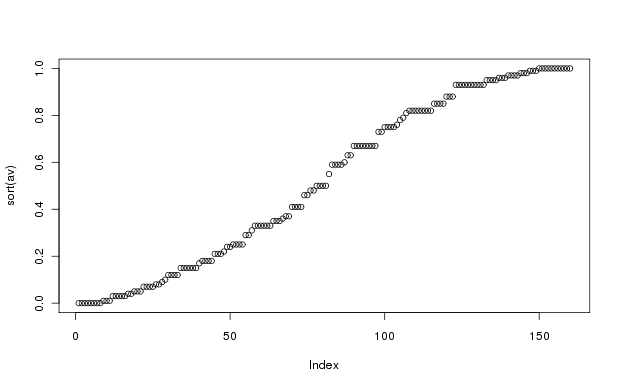
The distribution of aspect values shows a slight sine wave configuration. This is to be expected; the actual aspects are almost perfectly uniformly distributed from 0 to 360 degrees, so that the cos conversion results in the slight wave-like distribution. Aspect value is a very simple attempt to convert aspect in degrees from a circular variable to a linear (or at least monotonic) variable representing "coolness" that is suitable for statistical analysis. As explained in Roberts and Cooper (1989), the cos transformation is to convert aspect into solar radiation equivalents, and the correction of 30 degrees reflects the relative heat of the atmosphere at the time the peak radiation is received. Accordingly, the maximum value of av (=1.0) occurs at 30 degrees aspect, and the minimum (=0.0) at 210 degrees aspect. Of course, actual radiation loads are determined by latitude and slope as well as aspect, so the representation is over simplified.

Joint Distributions

To look at joint distributions of variables, simply specify one variable as the X axis, and a second variable as the Y axis. The vectors must be the same length. For example,
plot(av,elev) # to see the joint distribution

The joint distribution of elevation and aspect values is pretty good, and we should be able to employ both variables in analyses without worrying about correlation problems. If desired, the actual correlation can be tested easily.

Note: cor() computes a Kendall (parametric) or Spearman's (non-parametric) test where the output is 0 for no correlation and 1 for perfect correlation.

cor(av,elev)
[1] 0.09244026
Sometimes we're interested in how two variables co-occur given a third variable. R has an elegant solution to this problem called a coplot, but for now we will simply make separate plots depending on the variables of interest. For example, in Bryce Canyon we might be interested in how the joint distribution of elevation and aspect value varies as a function of soil depth. The simplest approach to this problem is to split the graphic page into two panels as follows:
par(mfcol=c(1,2)) # to get a double plot
The par(mfrow=c(1,2)) specification requires a little explanation. First, the par() function sets numerous graphics parameters (or "par" for short). The specific parameter to be set is passed as an argument to the function. So, mfrow stands for "multi-figure by rows", and the c(1,2) specifies "one row, two columns". Accordingly, we will get a double figure with one panel to the left of the other. For example, 

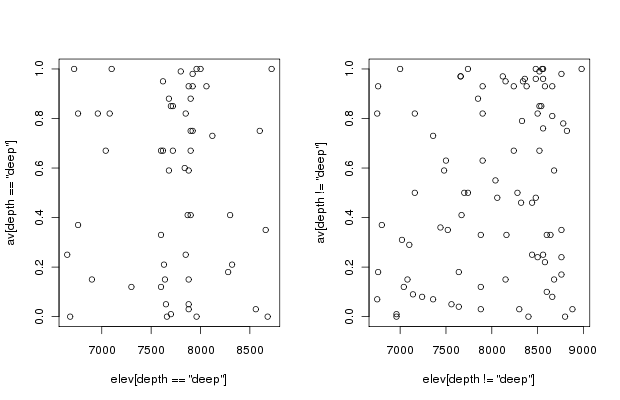
plot(elev[depth=='deep'],av[depth=='deep'])  # to see the joint distribution 

                                             # on deep soil



plot(elev[depth!='deep'],av[depth!='deep'])  # to see the joint distribution 

                                             # on shallow soil

par(mfcol=c(1,1)) # return to single plots

Alternatively, numerous small panels get difficult to read, and a good alternative is the box plot. 


boxplot(elev~depth)   # produces a simple visualization of elevation 

                      # by soil depth

The syntax of the boxplot() function is interesting, and is something we'll see often in other contexts. The ~ character is R for "as a function of" so that boxplot(elev~depth) means plot elev as a function of depth. The boxplot will plot one box for each possible value of depth, which in this case is only two. Later on we'll see many examples of ~ meaning "as a function of."

I did not get the t-test below to work with this dataset and stopped here.

Often the simple boxplot is enough to warn us that the distribution of one variable is related to another, but we can easily check for independence with a t-test.

t.test(elev~depth,var.equal=FALSE)

        Welch Modified Two-Sample t-Test



data:  elev[depth == "deep"] and elev[depth != "deep"] 

t = -3.0848, df = 135.07, p-value = 0.0025 

alternative hypothesis: true difference in means is not equal to 0 

95 percent confidence interval:

 -482.4255 -105.5039 

sample estimates:

 mean of x mean of y 

  7731.429  8025.393
The call to t.test() should seem simple by now. t.test() is the name of the function, and we're using the same syntax that we used in the boxplot. The var.equal=FALSE argument means not to assume equal variances in the two distributions (I tested, they're not). The upper part of the output is simple enough, and reports the value of Student's t, the degrees of freedom, and the associated p-value. Obviously, in this case, deep soils do not occur at the same mean elevation as shallow soils. In fact, as reported a few lines later, the mean for deep soils is 7731 feet, and for shallow soils 8025 feet, and the 95% confidence interval of the difference between them is 105 and 482 feet. The difference is less than we would expect from the boxplots, perhaps, because the distribution of elevations on shallow soils is skewed, making the mean significantly lower than the median, which is the bar indicated on the boxplot. T tests have lots of assumptions that complicate their interpretation (although as done here, not equal variance), and our use is simply to reinforce the idea that we will have to use caution interpreting the meaning of elevation and soil depth without accounting for the other.

For the nominal (categorical) data we are pretty much limited to table output. We can look at the number of plots on each class easily, for example:

table(pos) to see the distribution of topographic positions:

table(pos)

 bottom low_slope mid_slope ridge up_slope 

     20        33        54    18       35
or table(pos,depth) to see the joint distribution of soil depth by topographic position:
table(pos,depth)

          deep shallow 

   bottom   13       6

low_slope   14      14

mid_slope   18      31

    ridge    5      12

 up_slope    6      26
Similar tables can be produced (in more than two dimensions if desired) for other nominal variables.

A little later we'll be analyzing the distribution of species or vegetation composition as a function of environmental variability. Some of these analyses will be sensitive to the degree of correlation or independence among our environmental explanatory variables. For now, we can evaluate the dependence among categorical variables using a function called tabletest(). Simply cut and paste the function into your session: 



tabletest <- function(x, y)

{

        tmp1 <- table(x, y)

        tmp2 <- loglin(tmp1, list(1, 2), fit = T)

        list(dep = (tmp1 - tmp2$fit)/tmp2$fit, p = (1 - pchisq(tmp2$pearson,

                tmp2$df)))

}
tabletest() requires as arguments the two variables to be compared. For example,
tabletest(pos,depth)

2 iterations: deviation 7.62939e-06 

$dep:

                 deep     shallow 

   bottom  0.77161640 -0.48551151

low_slope  0.29464275 -0.18539317

mid_slope -0.04883387  0.03072694

    ridge -0.23844546  0.15003318

 up_slope -0.51450896  0.32373613



$p:

[1] 0.00546281
For now, ignore the first line of output about iterations and deviation. The primary outputs of interest are $dep and $p. The first is a table of relative deviations from expectation, i.e. (obs-exp)/exp. This table shows, for example, that there were many more plots on deep soils and bottoms than expected, while deep soils on up_slopes were much less common than expected. The $p gives the Chi-square statistic for deviations from expectation, given the appropriate degrees of freedom.

Obviously, soil depth and topographic position are not independent in our data set, and we will have to be careful about attributing effects to one without accounting for the other.

Let's look at the distribution of vegetation on the environment.

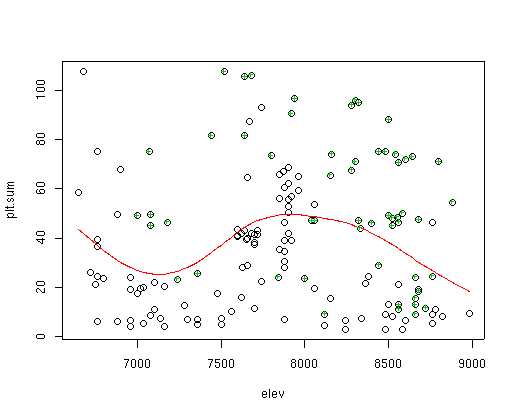
plot(elev,plt.sum) # to see if total cover varies as a function of elevation

To anticipate a future lab (Lab 5), we can fit a line (shown in red) to the plot cover data as a function of elevation as follows:

lines(sort(elev),fitted(gam(plt.sum~s(elev)))[order(elev)],col=2)

I won't attempt to explain all of that line in this lab, but it is a plot of a Generalized Additive Model (GAM) fit of plot cover to elevation. It's significant (P<0.001), but not terribly strong (pseudo R^2 = 0.13). We can highlight specific sample plots in the figure as follows:

points(elev[cover[,3]>2],plt.sum[cover[,3]>2],pch="+",col=3)
to see the distribution of sites where species 3 has more than 2 percent cover superimposed on the previous graph.

By varying the size of the plotted symbol, we can add dimensions to the plotted data easily. For example, the plot below has elev on the X axis, av on the Y axis, and slope plotted in different sized symbols by quartiles. 


plot(elev,av,type='n') 

          #  plot with no symbols type='n')



points(elev[slope<2],av[slope<2],pch=16,cex=0.75)                  

          # plot the first quartile in small symbols



points(elev[slope>=2&slope<3],av[slope>=2&slope<3],pch=16,cex=1.5) 

          # plot the second quartile slightly larger



points(elev[slope>=3&slope<5],av[slope>=3&slope<5],pch=16,cex=2)   

          # third quartile larger yet



points(elev[slope>=5],av[slope>=5],pch=16,cex=3)                   

          # last quartile largest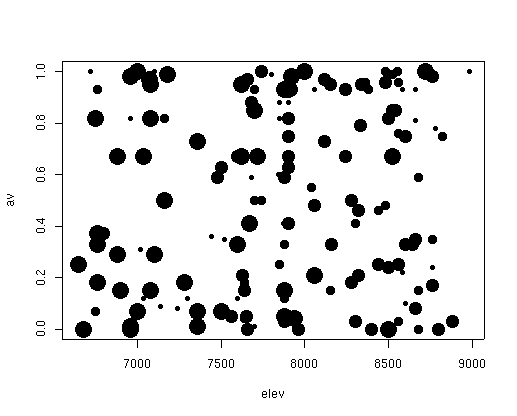

We can certainly make more creative and informative graphs by combining colors with sizes and shapes of plotting characters, but I'll leave that for now and introduce new graphics as the need arises.

Let's move on to Lab 3.